Research

Overview

I work in the field of algebraic combinatorics with a focus on combinatorial models of representations of Lie algebras. This pertains mainly to the use of combinatorial structures to encode complex algebraic objects and then make computations and conclusions using combinatorial techniques. The idea is that the combinatorial models are simpler to manipulate than the original algebraic object, but maintain all of the structure.

Main Algebriac Structure: Kashiwara Crystals

Crystal bases were independently discovered by Kashiawara and Lusztig in the early 1990’s as a means of deciphering nice combinatorial properties of representations of quantum groups (noncommutative analogs of Lie groups) and are the result of taking the limit of the quantum group’s parameter q to zero. Not only do these crystals have very nice combinatorial structure, as they can be modeled by colored directed graphs, but they also encapsulate all of the structure of the corresponding representation. The edges of these graphs are colored by crystal operators which are related to the corresponding Chevalley generators.

Use of Software:

In research pertaining to these combinatorial models, it is often useful to write software to encode the structure. Such software is used in many stages of research: the development of the combinatorial model, testing to make conjectures, and even to give insight as to how to prove those conjectures.

The use of SageMath has been an integral part of every project that I have worked on. See below for an example of how it nicely displays crystal graphs.

sage: view(crystals.Tableaux(['A',3],shape=[2,1]))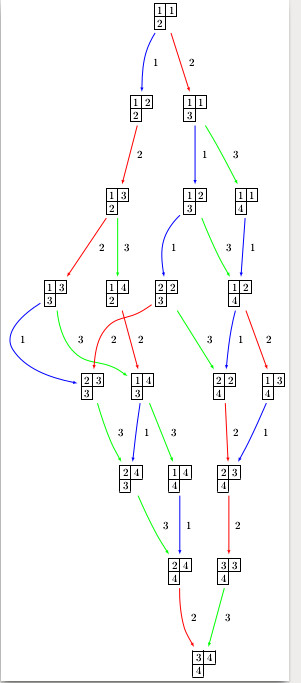

Room for Undergraduate Involvement:

My views concerning the inclusion of students in research are similar to those I hold in my classrooms: everyone learns differently and a main role that we hold as educators is to help students excel by offering a multitude of modalities to match their individual strengths. Our students come from diverse backgrounds with varying mathematical experiences. It is our job to meet them at their level and provide them with the opportunities needed to grow.

– For students who are algorithmic learners, we can present research in this field through the use of coding.

– For those who are visual learners, we can start with the fillings of Young diagrams.

– For students who are spatial learners, we can start with reflections and build up the field through root systems.

Research in mathematics is often limited to students who excel in certain proof writing courses. My hope is that we can take advantage of the very nature of this field to offer opportunities to a greater student audience. We can show students that their strengths can be math strengths, even if they are not traditionally deemed as such.